MGrayson
Subscriber and Workshop Member
This is a pure lecture post. If I were modern, I'd have a YouTube channel and put it there. But I'm old fashioned and like pictures. I want to look at what happens inside your camera at time steps of a few trillionths of a second. I mean, who wouldn't? The time it takes light to leave the rear element of the lens and smack into your sensor is about a ten billionth of a second. All the focusing and diffraction is done by the time the shutter has been open for another ten billionth of a second (fast shutter!), and the ensuing 1/1000 second exposure lets in a column of light 300 kilometers long. Those extra million nanoseconds do pretty much the same thing that the first nanosecond did, so we'll ignore them.
In the interest of visibility, I'm going to hugely increase the wavelength of the light. Instead of half a micron (5,000 Å), I'm going to use about 2.5mm, or 5,000 times as long - we're talking 120 GHz. Above WiFi frequencies, but not hugely. As you no doubt recall from our previous diffraction discussion, the longer the wavelength, the bigger the blob, so we'll hit diffraction limits at pretty big apertures.
What will be our subject? A point of light. A star. Exciting, huh? Light waves radiate from this star in concentric spheres, but by the time they get here, the spheres might as well be planes. Over the surface of your front element, that sphere will deviate from planar by a number with 29 zeroes after the decimal place. Flat. At this point, you might be asking yourself "Why do they stay flat?". Well, as anyone who has used a long lens or a telescope can tell you, they DON'T stay flat. Because air sucks! But why is it even remotely flat? How does the light know to DO that?
We think of light as going straight through transparent stuff like air and glass, maybe with some bending, but it isn't that simple. Light particles (Einstein was once offered an academic job DESPITE the fact that he believed in these ridiculous things called photons) travel about a millionth of an inch through air, and much less through glass, before they "interact" with the stuff they're going through. And every time they do, there's a chance of that light rushing off in some new direction. Thanks to Quantum Mechanics, we can say that the light is running off in ALL directions at once. So what keeps the waves lined up? Think about a dozen or so teenage boys standing in a line in swimming pool. If one of them jumps up and down, waves will radiate from him in all directions. If all of them jump up and down in sync, waves will spread out from them in a line, at least away from the ends of the line of boys. Why? Because if you are facing them from 5 feet away and take a step to your right, the line of boys will look the same. At least the ones close enough to you to be causing waves. The whole line parallel to the boys will be waving up and down in sync. This will not be true if you are near the end of the line (dramatic foreshadowing music).
Of course, we can do the math, observe that the Wave Equation (amazingly, the equation for waves) is linear, and so sums of solutions are solutions, and ... but I was hoping that the image of rowdy teenagers would be more compelling.
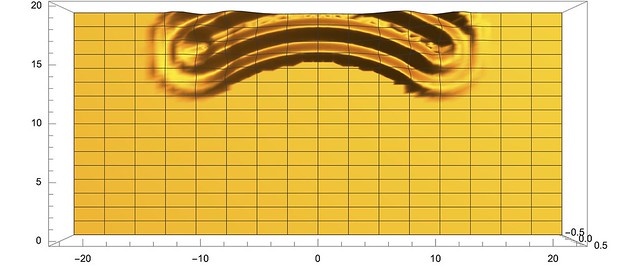
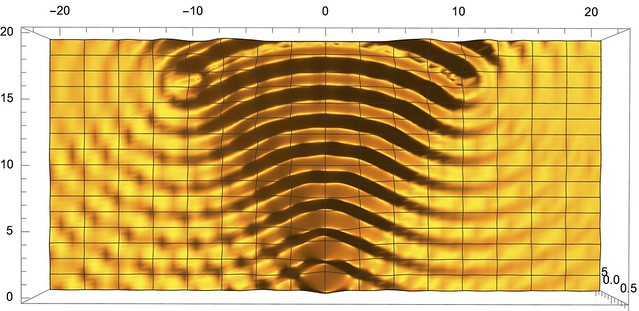
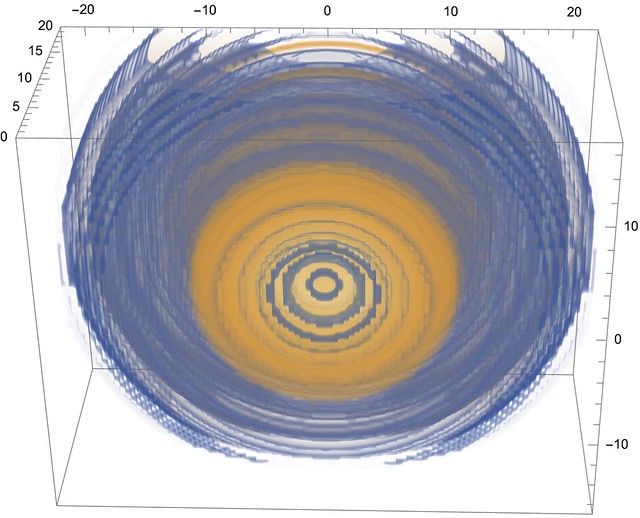
So to figure out what is happening when light first enters your camera (remember the camera?) we need to know what one boy jumping up and down does to the water, figure out where all the boys are, and add up their waves. As anyone who has thrown a pebble out into a still pond knows, circular ripples radiate outwards. A bit of physics tells us how the heights of the ripples change as they spread, and that's what we use for our one boy jumping, or, equivalently, light hitting one point at the entrance to our camera.
This is going to be long, and the pictures are about to start... (end of part 1)
In the interest of visibility, I'm going to hugely increase the wavelength of the light. Instead of half a micron (5,000 Å), I'm going to use about 2.5mm, or 5,000 times as long - we're talking 120 GHz. Above WiFi frequencies, but not hugely. As you no doubt recall from our previous diffraction discussion, the longer the wavelength, the bigger the blob, so we'll hit diffraction limits at pretty big apertures.
What will be our subject? A point of light. A star. Exciting, huh? Light waves radiate from this star in concentric spheres, but by the time they get here, the spheres might as well be planes. Over the surface of your front element, that sphere will deviate from planar by a number with 29 zeroes after the decimal place. Flat. At this point, you might be asking yourself "Why do they stay flat?". Well, as anyone who has used a long lens or a telescope can tell you, they DON'T stay flat. Because air sucks! But why is it even remotely flat? How does the light know to DO that?
We think of light as going straight through transparent stuff like air and glass, maybe with some bending, but it isn't that simple. Light particles (Einstein was once offered an academic job DESPITE the fact that he believed in these ridiculous things called photons) travel about a millionth of an inch through air, and much less through glass, before they "interact" with the stuff they're going through. And every time they do, there's a chance of that light rushing off in some new direction. Thanks to Quantum Mechanics, we can say that the light is running off in ALL directions at once. So what keeps the waves lined up? Think about a dozen or so teenage boys standing in a line in swimming pool. If one of them jumps up and down, waves will radiate from him in all directions. If all of them jump up and down in sync, waves will spread out from them in a line, at least away from the ends of the line of boys. Why? Because if you are facing them from 5 feet away and take a step to your right, the line of boys will look the same. At least the ones close enough to you to be causing waves. The whole line parallel to the boys will be waving up and down in sync. This will not be true if you are near the end of the line (dramatic foreshadowing music).
Of course, we can do the math, observe that the Wave Equation (amazingly, the equation for waves) is linear, and so sums of solutions are solutions, and ... but I was hoping that the image of rowdy teenagers would be more compelling.
So to figure out what is happening when light first enters your camera (remember the camera?) we need to know what one boy jumping up and down does to the water, figure out where all the boys are, and add up their waves. As anyone who has thrown a pebble out into a still pond knows, circular ripples radiate outwards. A bit of physics tells us how the heights of the ripples change as they spread, and that's what we use for our one boy jumping, or, equivalently, light hitting one point at the entrance to our camera.
This is going to be long, and the pictures are about to start... (end of part 1)
Last edited: